Việc đạt được công thức hạ bậc sin 2x là rất quan trọng trong toán học. Công thức này không chỉ là một biến đổi được phép mà còn có nhiều ứng dụng hữu ích để giải quyết các bài toán phức tạp hơn. Bài viết sẽ nói về nội dung của công thức, cách nó được sử dụng và những lợi ích của việc sử dụng nó.
1. Công thức hạ bậc sin 2x
Trong cả giác đại lượng và số lượng , công thức hỗ trợ giảm độ phức tạp của các biểu thức chứa hàm số giác .
Định nghĩa công thức hạ bậc
- Một trong những công thức cơ bản trong giác độ là công thức cấp bậc sin 2x:
- [ \sin(2x) = 2 \sin(x) \cos(x) ]
- Công thức này cho phép chúng tôi biến một số giác độ có cấp cao hơn , được hiển thị ở cấp 2, thành sự kết hợp của các hàm số cấp thấp hơn. Điều này rất hữu ích trong nhiều lĩnh vực toán học.
Tại sao cần hạ bậc?
- Các bài toán phức tạp, đặc biệt là tính toán phân tích hoặc đạo hàm , có thể được đơn giản hóa thông qua cấp bậc công việc. Việc hỗ trợ hạ cấp để xử lý các biểu thức phức tạp khi làm việc với các hàm số giác .
Mối liên hệ với các công thức lượng giác khác
Công thức cấp bậc liên kết chặt chẽ với các công thức giác giác khác, có ý nghĩa như
- Công thức tổng hợp
- Công thức của hiệu
- Cơ sở đẳng cấp không đổi về giác độ
- Việc giải quyết các vấn đề toán học từ đơn giản đến phức tạp có nhiều khả năng hơn khi hợp nhất các công thức này .

2. Ứng dụng công thức hạ bậc sin 2x trong giải toán
Công thức hạ tầng sin 2x không chỉ là lý thuyết mà còn có nhiều ứng dụng thực tế trong các bài toán mà học sinh thường làm .
Giải phương trình lượng giác
- Giải thích các phương pháp lượng giác là một trong những phương pháp sử dụng phổ biến nhất của công thức cấp bậc 2x . Chúng tôi có thể sử dụng công thức này để chuyển đổi sang dạng dễ hiểu hơn khi gặp các phương thức có dạng sin hoặc cos với cấp cao.
- Tiện ích, chúng tôi có thể biến phương thức sin(2x) = 0,5 thành:
- [ 2 sin(x) = 0.5 và cos(x) = 0.5 ]
- Do đó, chúng tôi có thể dễ dàng tìm thấy giá trị x.
Tính tích phân
- Các hàm số giác phải được tính toán phân tích . Mặt khác, chúng tôi có thể đưa ra các hàm số một cách dễ dàng hơn bằng cách sử dụng công thức cấp độ
- Dược phẩm, ta có thể viết lại thành 2 sin(x) cos(x) khi muốn tính phân tích của sin(2x). Điều này cho phép chúng tôi sử dụng nhiều phương pháp tính toán .
Phân tích đồ thị hàm số
- Trong phân tích sơ đồ của các hàm số , công thức hạ cấp cũng có lợi. Việc giảm cấp sẽ giúp tìm kiếm các điểm cực trị hoặc giao điểm trên đồ thị.
- Tăng cường tư duy logicChúng tôi có thể đưa ra các nhận xét chính xác hơn bằng cách chuyển đổi về dạng thấp hơn .
3. Ý nghĩa của công thức hạ bậc sin 2x
Đặc tính của số lượng giác .Công thức hạ tầng 2x có nhiều ý nghĩa sâu sắc hơn chỉ là một công cụ toán học .
- Khám phá tính chất hàm số lượng giác: Cửa ngõ giúp họ khám phá các tính chất của hàm số giác là công thức hạ cấp . Chúng ta có thể hiểu được các giác độ khác bằng cách hiểu công thức này.
- Ứng dụng trong khoa học và kỹ thuật: Các lĩnh vực khoa học và kỹ thuật có rất nhiều chế độ về số lượng giác. Công thức cấp bậc cho phép các nhà khoa học tính toán các bài toán phức tạp , quy trình sản xuất hoặc mô phỏng các biểu tượng tự nhiên tối ưu hóa .
- Phát triển tư duy logic: Nắm vững công thức hạ tầng 2x cũng giúp học sinh phát triển tư vấn duy logic và khả năng giải quyết vấn đề . Khả năng phân tích và biến đổi khi đối mặt với các phức tạp toán học sẽ giúp học sinh tự tin hơn trong việc tìm ra lời giải .
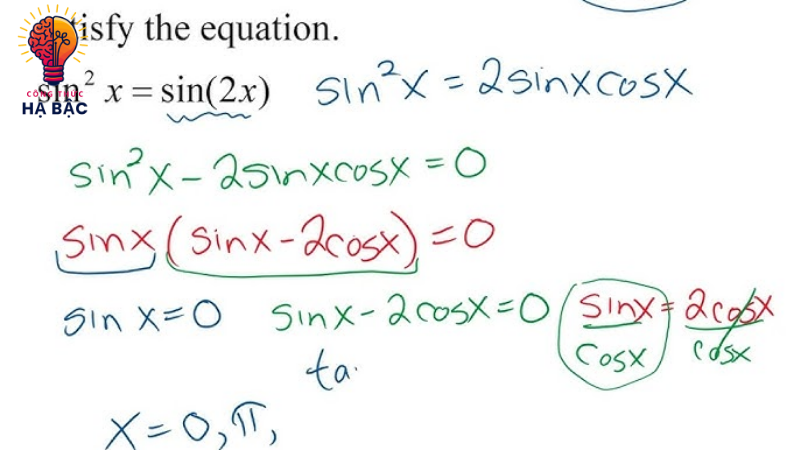
4. Cách sử dụng công thức hạ bậc sin 2x
Khi bạn đã quen thuộc với khái niệm về công thức cấp bậc, bước tiếp theo là biết cách áp dụng nó trong thế giới thực tế.
Bước 1: Nhận diện bài toán
- Trước đó, bạn phải xác định xem bài toán của mình có chứa các hàm số giác với bậc cao hay không . Nếu trường hợp đó hợp lý , hãy xem xét việc áp dụng công thức hạ tầng .
Bước 2: Chọn công thức phù hợp
- Sau khi xác định , hãy chọn công thức bậc phù hợp để thay đổi biểu thức . Công thức được sử dụng cho sin (2x):
- [ \sin(2x) = 2 \sin(x) \cos(x) ]
Bước 3: Tiến hành tính toán
- Cuối cùng, sau khi thay đổi biểu thức , bạn tiến hành tính toán theo cách thông thường. Nếu cần thiết để đạt được kết quả cuối cùng, có thể áp dụng nhiều công thức khác ..
- Bạn có thể trở thành một người thành phố sâu trong công việc áp dụng công thức hạ tầng sin 2x vào các bài toán khác nhau bằng cách thêm thủ công ba bước này.
5. Ví dụ minh họa về công thức hạ bậc sin 2x
Ví dụ 1: Giải phương trình đơn giản
Giả sử bạn có phương trình:
- [ \sin(2x) = 0.5 ]
- Áp dụng công thức hạ bậc:
- [ 2 \sin(x) \cos(x) = 0.5 ]
- Chia cả hai vế cho 2, ta có:
- [ \sin(x) \cos(x) = 0.25 ]
- Bây giờ, bạn có thể giải phương trình này bằng nhiều phương pháp khác nhau.
Ví dụ 2: Tính tích phân
Ta cần tính tích phân sau:
- [ \int \sin(2x) dx ]
- Áp dụng công thức hạ bậc:
- [ \int 2 \sin(x) \cos(x) dx ]
- Sử dụng phương pháp biến đổi phù hợp, bạn sẽ nhận được kết quả mong muốn.
6. Lợi ích của việc biết công thức hạ bậc sin 2x
Nắm vững công thức cấp bậc sin 2x có lợi cho học sinh và người học toán.
- Tăng cường khả năng giải quyết vấn đề: Người học có thể linh hoạt hơn khi giải quyết các bài toán phức tạp bằng cách sử dụng các công thức hạ tầng . Bạn có các công cụ hữu ích trong tay nên bạn sẽ không lo lắng khi gặp các bài toán mới.
- Cải thiện hiệu suất học tập: Nắm bắt các công thức cơ bản như hạ tầng giúp học sinh học tốt hơn. Kiến thức chắc chắn sẽ giúp bạn tiếp cận các chủ đề khác nhanh hơn và dễ dàng hơn .
- Ứng dụng đa dạng trong thực tế: Cuối cùng, công thức cấp bậc không chỉ được sử dụng trong học đường mà còn được sử dụng trong nhiều lĩnh vực khác nhau, ví dụ như vật lý, kỹ thuật và kinh tế. Điều này sẽ giúp bạn thành công trong tương lai.
7. Phân tích sâu về công thức hạ bậc sin 2x
Chúng tôi đã biết về công thức và ứng dụng của nó. Tuy nhiên, để nắm được công thức hạ cấp 2x , bạn cần tìm hiểu thêm .
- Tính chất chu kỳ: Tính chất chu kỳ của hàm số giác được liên kết với công thức cấp bậc sin 2x . Tuy nhiên, với công thức này, hàm số có chu kỳ 2π/2 = π. Điều này sẽ ảnh hưởng đến việc phân tích sơ đồ và giải phương pháp .
- Sự liên kết giữa các hàm số: Điều này rất quan trọng trong việc nghiên cứu các tính chất giác quan vì công thức hạ cấp cho thấy sự liên kết giữa sin và cos . Cuối cùng, không thể phủ nhận rằng công thức hạ cấp rất quan trọng trong các lĩnh vực khác như tín hiệu , kỹ thuật điện và mô phỏng vật vật lý .Trong một số toán , việc chuyển đổi giữa các số sẽ giúp bạn tìm ra lời giải nhanh hơn.
- Vai trò trong các lĩnh vực khác: Những kiến thức này không chỉ có giá trị học thuật mà còn có những ứng dụng thực tế .
8. Kết luận
Công thức cấp bậc sin 2x là một phương pháp giác độ và toán học mạnh mẽ. Nắm vững và hiểu rõ công thức này không chỉ giúp bạn giải quyết các bài toán phức tạp mà còn mở ra nhiều cách mới để nghiên cứu và ứng dụng toán học vào cuộc sống. Bạn có thể hiểu rõ hơn về công thức cấp bậc 2x nhờ bài viết này .
Công thức hạ tầng sin 2x không chỉ là công cụ hữu ích để đơn giản hóa các biểu thức giác độ mà còn là chìa khóa mở ra cách tiếp cận các bài toán phức tạp một cách dễ dàng hơn. Khi hiểu rõ và áp dụng tốt, bạn sẽ thấy toán học không đáng sợ mà thực sự thú vị, như một phương pháp chữa bệnh “bệnh hắc lào” chống mặt với các con số và công thức, chi tiết xin truy cập website:congthuchabac.comxin cảm ơn!