Công thức hạ bậc cos 2 là một trong những công thức toán học quan trọng nhất. Nó được sử dụng rộng rãi trong nhiều lĩnh vực , từ kỹ thuật đến vật lý. Tuy nhiên, việc sử dụng công thức này có thể khó khăn và có thể dẫn đến một số sai sót phổ biến. Chúng tôi sẽ nói chi tiết về ý nghĩa của công thức hạ cấp cos 2, cách sử dụng nó và ba sai sót thường gặp khi sử dụng nó .
1. Công thức hạ bậc cos 2 là gì?
Mục tiêu của công thức cấp cos 2 là biểu thức hóa học đơn giản chứa hàm cos (2x). Đặc biệt, công thức này cho phép biểu diễn cos(2x) như một biểu thức chứa hàm cos(x).
Công thức hạ bậc cos 2
Công thức cấp cos(2x) = 2cos²(x) – 1
Trong đó:
- cos(2x) là hàm cosinus với góc 2x
- cos(x) là hàm cosinus với góc x
Một biểu thức chứa hàm cos(x) được tạo ra bởi công thức này. Điều này rất hữu ích trong các bài toán về tam giác và dao động.
Cách suy ra công thức hạ bậc cos 2
Chúng ta có thể sử dụng các công thức lượng giác cơ bản để tìm ra công thức hạ bậc cos Về cụ thể:
- cos(2x) = cos²(x) – sin²(x)
- Sử dụng công thức: cos²(x) + sin²(x) = 1
- Thay vào, ta có: cos(2x) = 2cos²(x) – 1
- Đây là công thức hạ cấp cos 2 mà chúng tôi đã quen thuộc.
Ý nghĩa của công thức hạ bậc cos 2
- Công thức cấp cos 2 có một số ý nghĩa chính : Đơn giản hóa tính toán: Công thức này cho phép chúng ta mô tả hàm cos(2x) bằng một biểu thức chỉ chứa hàm cos(x). Khi tính toán, điều này rất hữu ích vì nó giúp tiết kiệm thời gian và công sức.
- Ứng dụng trong bài toán: Công thức này được sử dụng rộng rãi trong nhiều lĩnh vực, suy nghĩ như toán học, vật lý và kỹ thuật.
Ví dụ : nó có thể được sử dụng cho các bài toán về phân tích, dao động và chất của tam giác.
- Tính chất đặc biệt : Tính chu kỳ và mối liên hệ với các giác giác khác là một trong những tính chất đặc biệt của công thức cấp cos 2. Chúng
- ta có thể áp dụng công thức một cách hiệu quả hơn nếu chúng ta hiểu được các đặc điểm này. Tóm tắt lại, công thức hạ cấp cos 2 là một công cụ toán học vô cùng hữu ích có nhiều ứng dụng trong các lĩnh vực khoa học và kỹ thuật khác nhau.
2. Cách sử dụng công thức hạ bậc cos 2 trong toán học
bài toán học , từ đơn giản đến phức tạp , sử dụng công thức hạ tầng cos 2. Một ví dụ: cos 2 Đây là một số ví dụ về cách sử dụng công thức này:
Đơn giản hóa biểu thức chứa cos(2x)
- Đơn giản hóa các biểu thức chứa hàm cos(2x) là một trong những cách sử dụng phổ biến nhất của công thức hạ tầng cos 2.
- cos(2x) + 3cos(2x) = 4cos²(x) – 3
- Một ví dụ:Trong trường hợp này, cos (2x) được hiển thị dưới dạng một biểu thức chứa cos(x) bằng cách sử dụng công thức cấp cos 2. Điều này giúp tính
- toán trở nên đơn giản hơn và giúp thực hiện các phép tính tiếp theo trở nên dễ dàng hơn .
Tích phân các biểu thức chứa cos(2x)
- ( 2x) Khi tính tích các biểu thức chứa hàm cos(2x), công thức hạ cấp cos 2 cũng rất hữu ích.
- ∫cos(2x)dx = 1/2 ∫(2cos²(x) – 1)dx = 1/2 (sin(x) – x) + C
- Trong ví dụ này, chúng ta biến biểu thức chứa cos(2x) thành một biểu thức chứa cos(x) bằng cách sử dụng công thức cấp cos 2. Sau đó, chúng tôi có thể dễ dàng tính toán phân tích của biểu thức mới.
Tính chất của tam giác
Tam giác ABC có góc A = 2x, B = x và C = π – 3x. Độ dài cạnh c có thể được tìm thấy bằng cách sử dụng công thức hạ cấp cos 2 như sau :
- c² = a² + b² – 2ab*cos(2x)
- = a² + b² – 2ab*(2cos²(x) – 1)
- Do đó , công thức cấp cos 2 hỗ trợ công việc tính toán các chất của tam giác .
Ứng dụng trong vật lý và kỹ thuật
- Nó có thể được sử dụng trong các bài toán liên quan đến điện tích, quang học và dao động, ví dụ.Công thức hạ cấp cos 2 không chỉ được sử dụng trong toán học mà còn được sử dụng rộng rãi trong các lĩnh vực kỹ thuật và vật lý.
- Tóm tắt lại, công thức hạ cấp cos 2 là một công cụ toán học vô cùng hữu ích có nhiều ứng dụng trong các lĩnh vực khoa học và kỹ thuật khác nhau. Chúng tôi sẽ giải quyết các bài toán một cách hiệu quả hơn nếu biết cách sử dụng công thức này.
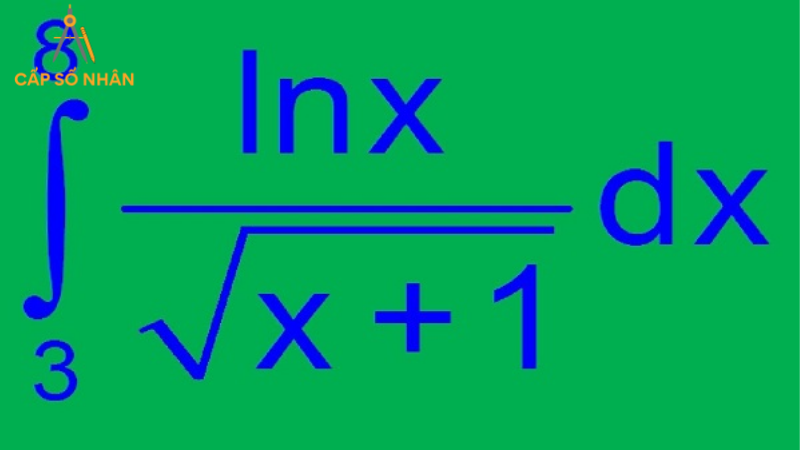
3. Ví dụ minh họa công thức hạ bậc cos 2
Chúng ta sẽ xem qua một số ví dụ cụ thể để hiểu rõ hơn về công thức cấp cos 2 và cách áp dụng nó .
Ví dụ 1: Đơn giản hóa biểu thức có cos(2x)
- Đơn giản hóa biểu thức sau: 4cos(2x) – 2sin(2x)
- cosine(x)Giải thích: Bằng cách sử dụng công thức cấp bậc cos 2, chúng ta có thể thấy rằng
- Hãy đơn giản hóa biểu thức sau: 4cos(2x) – 2sin(2x)
- Giải: Sử dụng công thức hạ bậc cos 2, chúng ta có: cos(2x) = 2cos²(x) – 1 sin(2x) = 2sin(x)cos(x)
- Thay vào biểu thức ban đầu, ta được: 4cos(2x) – 2sin(2x) = 4(2cos²(x) – 1) – 2(2sin(x)cos(x))
- = 8cos²(x) – 4 – 4sin(x)cos(x)
- = 8cos²(x) – 4 – 2sin(2x)
- Như vậy, chúng ta đã đơn giản hóa biểu thức chứa cos(2x) và sin(2x) thành một biểu thức chỉ chứa cos(x) và sin(x).
Ví dụ 2: Tính tích phân biểu thức chứa cos(2x)
- Tính ∫cos(2x)dx
- Giải: Sử dụng công thức hạ bậc cos 2, ta có: cos(2x) = 2cos²(x) – 1
- Thay vào biểu thức tích phân, ta được: ∫cos(2x)dx = ∫(2cos²(x) – 1)dx
- = 2∫cos²(x)dx – ∫dx
- = 2(1/2 * x – 1/4 * sin(2x)) – x + C
- = x – 1/2 * sin(2x) + C
- Vậy, tích phân của cos(2x) là x – 1/2 * sin(2x) + C.
Ví dụ 3: Tính chất của tam giác
- Cho tam giác ABC với góc A = 2x, B = x, C = π – 3x. Hãy tính độ dài cạnh c.
- Giải: Sử dụng công thức hạ bậc cos 2, ta có: c² = a² + b² – 2ab*cos(2x) = a² + b² – 2ab*(2cos²(x) – 1)
- Như vậy, chúng ta có thể tính được độ dài cạnh c dựa trên các góc của tam giác và công thức hạ bậc cos 2.
- Các ví dụ trên minh họa rõ ràng cách sử dụng công thức hạ bậc cos 2 trong các bài toán toán học và ứng dụng. Việc nắm vững công thức này sẽ giúp chúng ta giải quyết các bài toán một cách hiệu quả hơn.
4. Tính chất đặc biệt của công thức hạ bậc cos 2
Tính toán chu kỳCông thức hạ bậc cos 2 không chỉ được sử dụng phổ biến trong toán học mà còn có một số tính chất làm cho nó trở thành một công cụ vô cùng hữu ích.
Tính chu kỳ
Tính chu kỳ của công thức hạ bậc cos 2 là một đặc điểm của nó. Đặc biệt, chúng tôi có:
- cos(2(x + kπ)) = cos(2x)
- Theo đó, hàm cos(2x) có chu kỳ bằng π. Tóm lại, sau mỗi khoảng cách π trên trục x, giá trị của hàm sẽ lặp lại.
- Tính năng này rất hữu ích trong các trường hợp cần xác định hay biểu diễn các hàm có chu kỳ trong toán học và các ứng dụng khác.
Liên hệ với các hàm lượng giác khác
Các hàm lượng giác khác như sin(2x) và tan(2x) liên quan đến công thức hạ bậc cos 2. Về cụ thể:
- sin(2x) = 2sin(x)cos(x) tan(2x) = 2tan(x)/(1 – tan²(x))
- Hiểu rõ các mối liên hệ này sẽ giúp chuyển đổi giữa các hàm lượng giác dễ dàng hơn và áp dụng công thức hạ bậc cos 2 linh hoạt hơn.
Tính đối xứng
- Tính đối xứng của hàm cos(2x) cũng được hiển thị trong công thức hạ bậc cos 2.
- cos(-2x) = 2x cos
- Điều này cho thấy đồ thị hàm cos(2x) là một đường cong đối xứng đi qua trục Oy. Tính năng này rất hữu ích trong việc vẽ và phân tích đồ thị của các hàm lượng giác.
- Tóm lại, công thức hạ bậc cos 2 thể hiện một số tính chất đặc biệt của hàm cos(2x), ngoài việc là một công cụ tính toán hữu ích. Nắm vững các đặc điểm này sẽ giúp chúng ta áp dụng công thức một cách hiệu quả hơn trong các bài toán và ứng dụng.
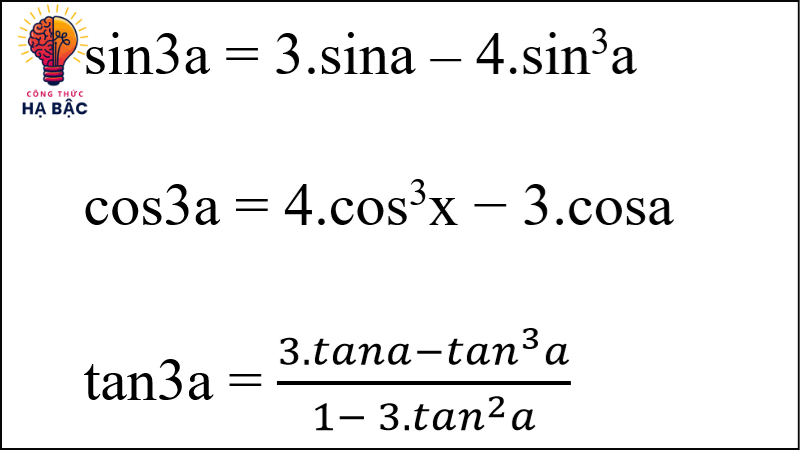
5. So sánh công thức hạ bậc cos 2 với các công thức khác
Công thức cho phép hạ bậc cos
So sánh công thức hạ bậc cos 2 với các công thức khác
- Khi nói đến công thức hạ bậc trong toán học, bạn phải nhớ đến sự tương tác giữa các hàm lượng giác. Công thức hạ bậc cos 2 là một trong nhiều công thức hữu ích mà chúng ta có, và việc so sánh nó với các công thức khác sẽ làm rõ sự khác biệt của nó và ứng dụng của nó.
Khác biệt với công thức sin 2
- Mặc dù cả hai công thức hạ bậc cos 2 và sin 2 đều dựa trên hàm lượng giác cơ bản, nhưng chúng mô tả các khía cạnh khác nhau của góc khi so sánh chúng.
- Công thức sin(2x) = 2sin(x)cos(x) cho phép tính giá trị của sin ở một góc gấp đôi bằng cách tích hai hàm cos và sin ở cùng một góc. Tuy nhiên, công thức hạ bậc cos 2, cụ thể là cos(2x) = 2cos2(x) – 1, đã cho chúng tôi thấy hành vi của cosin khi diện tích của một góc được nhân đôi.
- Điều này rất quan trọng khi giải quyết các bài toán hình học hoặc vật lý liên quan đến sự dao động. Những bài toán này thường yêu cầu phân tích song song các chuyển động theo hướng khác nhau (sin và cos).
Tương quan với công thức tan 2
- Khi so sánh, cần lưu ý đến công thức hạ tầng tan 2 , ngoài các hàm sin và cos. Theo công thức tan(2x) = 2tan(x)/(1 – tan2(x)), chúng ta phải tính giá trị tang của một góc gấp đôi bằng cách tính giá trị của tan ở góc đầu tiên.
- Sự khác biệt chính nằm ở cách áp dụng . Khi làm việc , bạn thường cần chú ý đến điều kiện xác định . Điều này có thể không được xác định ở một số nơi . Tuy nhiên, việc sử dụng công thức hạ cấp cos 2 hoàn toàn có thể được thực hiện mà không cần phải lo lắng về tính xác định của hàm.
- Một điều thú vị là cả ba công thức (hạ cấp cos 2, sin 2 và tan 2) đều được tìm thấy mối liên hệ chặt chẽ với nhau, và việc hiểu rõ từng công thức sẽ giúp chúng ta giải quyết các bài toán phức hợp dễ dàng hơn.
Ứng dụng trong giải tích hàm
- Tầm quan trọng của công thức hạ bậc cos 2 trong giải tích hàm được chứng minh bằng cách so sánh nó với các công thức khác. Phần lớn các ứng dụng cần chuyển đổi giữa nhiều dạng hàm lượng giác để đạt được kết quả mong muốn.
- Chẳng hạn, trong trường hợp một vấn đề yêu cầu xác định giá trị cực đại hoặc cực tiểu của một hàm chứa cos(2x), việc sử dụng công thức hạ bậc cos 2 sẽ giúp đơn giản hóa biểu thức và làm cho việc tìm các điểm cực trị dễ dàng hơn. Đây là một thành phần rất quan trọng trong bất kỳ nghiên cứu hay ứng dụng liên quan đến tối ưu hóa.
- Tóm lại, trong số rất nhiều công thức khác trong toán học, công thức hạ bậc cos 2 nổi bật nhất. Hiểu rõ các mối quan hệ giữa các công thức khác nhau sẽ giúp chúng ta sử dụng chúng hiệu quả hơn và cải thiện khả năng phân tích và giải quyết bài toán trong nhiều lĩnh vực.

6. Những sai lầm thường gặp khi áp dụng công thức hạ bậc cos 2
thức hạ tầng cos 2 rất hữu ích , nhưng người học cũng có thể gặp phải những vấn đề và sai sót. Những lỗi này sẽ giúp học sinh cải thiện kỹ năng sử dụng công thức một cách chính xác và hiệu quả .
Nhầm lẫn trong dấu hiệu
- Một trong những sai phổ biến nhất khi sử dụng công thức cấp độ cos 2 là nhầm lẫn về các dấu hiệu của các thành phần trong công thức . Điều này dẫn đến sai sót trong tính toán , ảnh hưởng đến kết quả.Nhiều người có thể quên dấu âm ở cuối khi chuyển đổi từ cos(2x) sang 2cos2(x) – 1, hoặc họ có thể không chú ý đến các thành phần khác có thay đổi hay không .
- Để tránh trường hợp này, người học nên kiểm tra lại biểu thức liên tục sau mỗi lần chuyển đổi để đảm bảo rằng tất cả các thành phần đều được giữ nguyên.
Không áp dụng đúng điều kiện
- Khi sử dụng công thức cấp bậc, một số học sinh cũng không chú ý đến các điều kiện của hàm lượng giác . Dược phẩm , trong một số trường hợp nhất được xác định, suy ra giới hạn như khi tính toán tan(2x), người học có thể bỏ qua những điểm mà tan không xác định rõ ràng.
- Không chú ý rằng điều này có thể dẫn đến những kết luận sai lệch hoặc giải bài toán không hợp lệ. Do đó, điều quan trọng phải được chú ý đến điều kiện xác định cũng như khoảng giá trị của các hàm giác .
Thiếu đi các bước trung gian
- Kết quả:Khi giải toán bằng công thức hạ cấp cos 2, bạn cũng bỏ qua các bước trung gian . Người học có thể cố gắng làm mọi thứ trong đầu mà không viết ra giấy; điều này có thể dẫn đến nhầm lẫn và khó theo dõi các bước giải quyết.
- Để tránh tình trạng này, người học nên xác định các bước thay thế giá trị và rút gọn biểu thức. Điều này không chỉ tăng tính chính xác mà còn giúp bạn cảm nhận được tự động hơn khi giải quyết các bài toán phức tạp .
- Nhìn chung, việc nhận diện và hiểu rõ những sai lầm thường xảy ra khi sử dụng công thức hạ bậc cos 2 sẽ giúp người học phát triển khả năng tư duy toán học của họ và giảm thiểu các lỗi không đáng có mà họ phải mắc phải trong quá trình học tập và làm việc.
7. Kết luận
Công thức hạ cấp cos 2 là một công cụ toán học quan trọng có thể được sử dụng trong nhiều lĩnh vực khoa học và kỹ thuật khác nhau. Công thức này có nhiều lợi ích cho người học và nhà nghiên cứu , bao gồm việc đơn giản hóa các biểu thức, tính phân tích và xác định độ dài trong tam giác.
Công thức hạ tầng cos 2 không chỉ là công cụ hữu ích để đơn giản hóa các biểu thức giác độ mà còn là chìa khóa mở ra cách tiếp cận các bài toán phức tạp một cách dễ dàng hơn. Khi hiểu rõ và áp dụng tốt, bạn sẽ thấy toán học không đáng sợ mà thực sự thú vị, như một phương pháp chữa bệnh “bệnh phong” chống mặt với các con số và công thức, chi tiết xin truy cập website:congthuchabac.comxin cảm ơn!